|

 |
|  | |||||||||||||||||||||||||||||||||||||||||||||
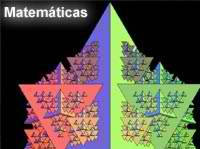
Noticias | Formales | Matemáticas«Con los fractales podemos poner orden al caos»La teoría de los fractales es considerada la tercera gran revolución científica, equiparable al descubrimiento de la Relatividad o de la Mecánica Cuántica. Los fractales permiten aportar lógica y orden dentro del aparente caos universal. Las aplicaciones de esta teoría son inmensas, ya que sirven para explicar el crecimiento de un tumor o la evolución de una costa Publicado: Lunes, 5/3/2007 - 15:17 | 6149 visitas.
Noticia publicada en Norte Castilla (España)
-¿Qué son exactamente los fractales? -Es un tipo de geometría que sirve para explicar los fenómenos caóticos, entendiendo por caos los sistemas que evolucionan en el tiempo. Por ejemplo, se podría obtener una explicación a la forma caprichosa de las nubes, los movimientos de la bolsa, los cambios en la demografía, el crecimiento de los tumores o el tratamiento de la osteoporosis. Los elementos caóticos son sistemas que dependen fuertemente de las condiciones iniciales, de forma que una pequeña variación en esas condiciones produce efectos impredecibles. -¿Qué supone que exista un orden para todo? -Hasta ahora, las matemáticas han estudiado menos el orden de los fenómenos aleatorios, porque explican mejor los fenómenos con orden que los aleatorios. Los fractales son imprescindibles, por ejemplo, para explicar dos fenómenos. El fenómeno frontera, que sirve, por ejemplo, para medir la longitud de una costa. El otro es el fenómeno del árbol, que es en el que se producen ramificaciones. -¿En qué nos va a afectar -A lo largo de toda la vida buscamos modelos. Con los fractales podemos modelizar la realidad, tenemos el poder de reproducirlo y saber cómo va a evolucionar en el tiempo. Si sabemos cómo va a ser la evolución de un tumor, por ejemplo, tendremos más oportunidades para detenerlo. Los fractales ya se usan para tratar la osteoporosis. -¿Cómo son los fractales? -Tienen dos características. Una es la autosemejanza: cada parte es similar al todo. La otra es la autorreferencia: cada parte está formada por elementos idénticos que forman parte de un orden inferior. -¿Cómo se explica que muchos científicos traten de explicar una teoría del caos y otros, la de los fractales? -En la ciencia hay muchas líneas de investigación. Einstein murió sin conseguir uno de sus grandes objetivos, que era lograr una teoría unificadora. Él no creía en el azar. «Dios no juega a los dados», decía. Pensaba que todo era producto de una causa-efecto. El matemático Borch le respondió: «no sólo juega con ellos, sino que en ocasiones los tira donde no podemos verlos».
| Noticias
Imágenes
Videos
Artículos
EntradasLibros
| ||||||||||||||||||||||||||||||||||||||||||||||


 Imagen: Tiggerfox Blog
Imagen: Tiggerfox Blog